La loi de Benford (loi du premier nombre) est souvent utilisée pour effectuer des tests de nature générale en analyse juricomptable de données. C’est loin d’être un test infaillible, mais il peut aider à détecter certaines anomalies dans des jeux de données sur lesquels il vaut parfois la peine de se pencher. En fait, en date d’aujourd’hui, ce test m’a permis de détecter une fraude qu’une seule fois, et c’était relativement minime en termes de valeur.
Pour les curieux, cela m’a permis de découvrir que la directrice des finances d’une entreprise payait son compte personnel d’électricité à l’aide de transferts électroniques provenant du compte bancaire de son employeur.
Le fondement de la loi de Benford repose sur le principe que la distribution du premier chiffre d’un ensemble de nombre sera naturellement similaire d’une population à l’autre. Ainsi, environ 30% des nombres commenceront par le chiffre 1, 17,6% par le chiffre 2, etc.
Je rentrerai dans les détails de cette loi et comment l’utiliser dans un autre billet. Ce que je veux toucher ici est l’importance à accorder à ce type d’analyse dont les résultats peuvent facilement porter à confusion. Afin d’illustrer le tout, regardons les deux graphiques suivants:
Graphique 1
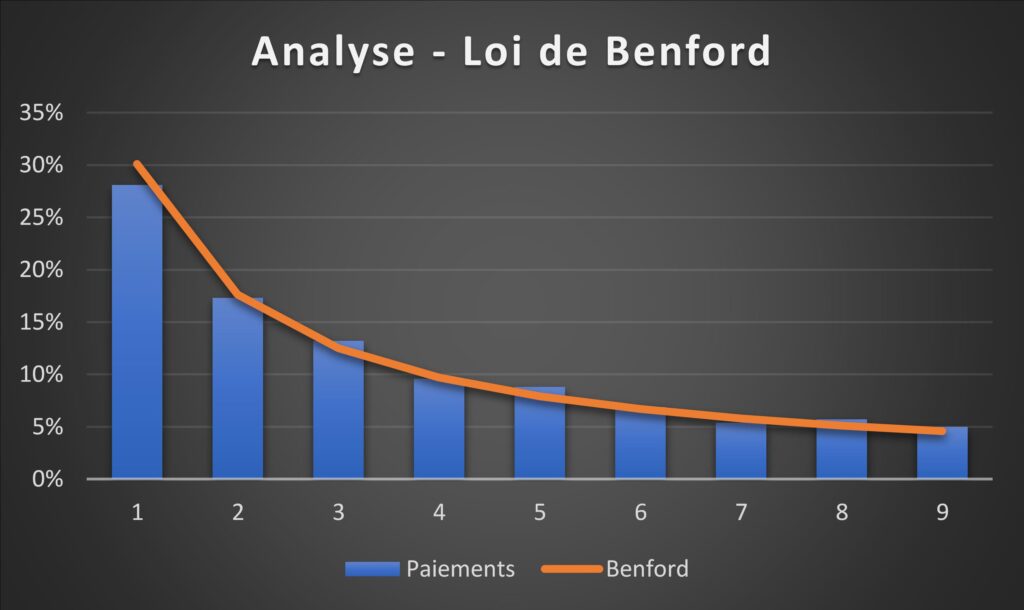
Dans ce premier graphique, nous pouvons remarquer que la répartition de la population suit la courbe attendue par la loi de Benford.
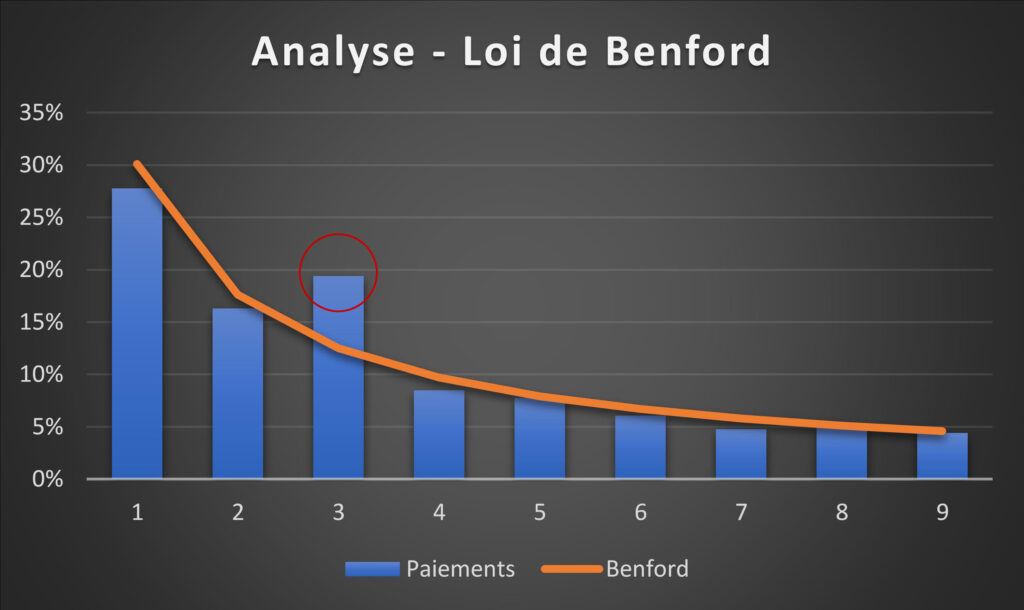
Graphique 2
Dans ce second graphique, nous notons que la proportion des nombres commencant par le nombre 3 est plus importante de ce qui est attendu selon la loi de Benford.
Ainsi, sur la simple base de ce test, le Graphique 1 ne semble démontrer aucune anomalie apparente, alors que le Graphique 2 présente une irrégularité potentielle.
Si je vous disais que dans les données utilisées pour générer le premier graphique se cache une fraude massive de 1 million de dollars et qu’il n’y a absolument rien d’anormal avec les données relatives au deuxième graphique? C’est pourtant le cas ici!
Les deux graphiques ont été générés à partir d’une population de 1000 paiements distincts. Sur ces 1000 transactions, le Graphique 1 en contient 315 dont le premier chiffre est 1. Même si la moyenne des paiements de ces 315 transactions est de 100$ et qu’il y a une seule transaction de 1,000,000$, cela n’a aucun impact significatif dans le résultat de ce test. Pourquoi? Puisque nous parlons d’une seule transaction sur 1000. Une fraude aussi flagrante sera assurément détectée à l’aide d’autres tests, mais sur la base de la loi de Benford, elle passerait totalement inaperçue.
En ce qui concerne les données du deuxième graphique, la proportion plus importante des paiements dont le premier nombre est 3est explicable par des paiements de passe de stationnement pour certains employés de la compagnie concernée. Cette dernière rembourse les frais mensuels de stationnement pour 10 de ses employés, ce qui créer donc 10 x 12 mois = 120 transactions débutant par le chiffre 3 sur un total de 1000. Ceci est suffisant pour créer la divergence présentée dans le Graphique 2.